12월 9일, 15주차 1강
부제: Data Flow Analysis
* 개인 공부를 위해 정리한 것입니다. 정확한 내용은 꼭 본인이 공부하는 교재를 참고하시기 바랍니다.
Reaching Definition Analysis
https://estudies4you.blogspot.com/2017/12/reaching-definitions-in-dataflow.html
이 모든 것을 이해하는데 지대한 도움을 준 글.
다만! 다른 자료들과 다르게 이 자료만 out의 초기화 값을 gen으로 설명하고 있음.
그런데 다른 자료들 다 찾아봐도 in, out은 모두 공집합으로 초기화하라고 하고 있음. 이부분에 주의할 것.
아래 ppt대로 설명하긴 하겠지만, 지금 한 번 쭉 정리하고 내 말로 한 번 설명하겠음
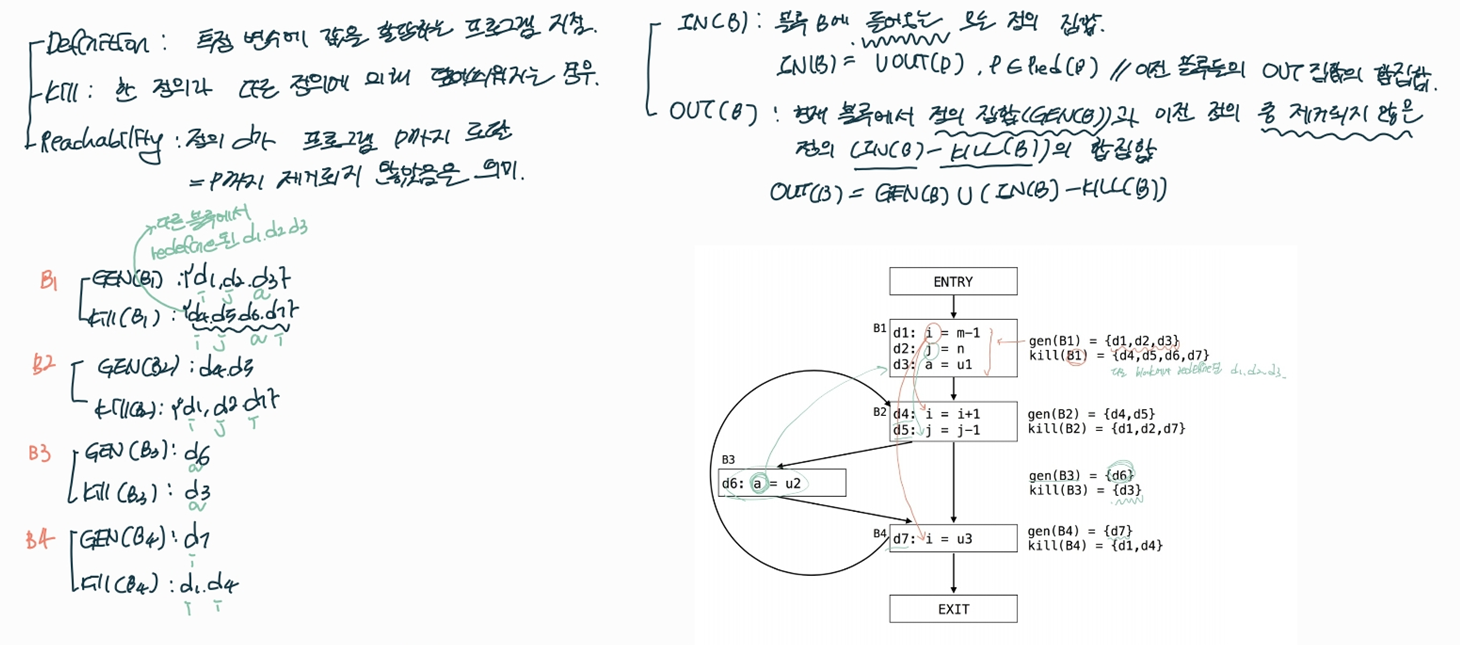
특정 변수에 값을 할당한 경우 "정의"가 되고, 특정 변수에 값을 또 할당하면 "kill"이 됨.
그래서 이 "정의"가 어떤 프로그램 지점까지 도달하기 위해서는 "kill"되지 않아야 함.
그래서 reaching definition analysis를 통해 "어떤 변수의 정의가 어떤 위치까지 도달하는가!"를 분석함
GEN과 KILL
분석에 앞서서 각 블록에서 어떤 "정의"가 일어나고, 그 정의가 어떤 지점에서 "죽는"지 파악해야 함
현재 블록에서 변수를 정의하는 모든 정의를 GEN, 이 블록 내 정의를 재정의하는 모든 것을 KILL
(블록 내에서 재정의될 수도 있음. 그럼 정의,재정의 둘다 kill 됨. 이하 ppt에서 예시 나옴)
손 필기를 참고하면 되는데, 블록 1을 예시로 들자면
블록1 내부에서 d1,d2,d3을 통해 각각 i,j,a가 정의됨.
블록2에서 d4,d5를 바탕으로 i,j를 재정의하고, 블록3에서 d6을 바탕으로 a를 재정의, 블록 4에서 d7을 바탕으로 i 재정의
그래서 KILL이 d4,d5,d6,d7이 되는 것임. 같은 방식으로 나머지 블록도 정의하면 됨.

Reaching Definition Analysis는 한 번에 이루어지지 않음. loop를 반복해야 함.
일단 모든 블록을 IN=공집합, OUT=공집합으로 초기화한다.
그 다음부터 단계적으로 작업을 반복한다.
각 블록에 대해 IN은 이 블록으로 들어오는 블록's OUT의 합집합 , 블록2는 블록1, 블록2는 블록1/4가 들어온다.
이때, 현재 블록으로 들어오는 블록들의 OUT 결과를 바탕으로 현재 블록들의 OUT을 구한다.
현재 loop를 돌면서 OUT값이 바뀌는 경우가 있는데, 그 값들까지 반영해서 현재 블록의 IN을 업데이트한다.
다만, 미래에 일어날 OUT을 예측해서 반영하거나 해서는 안됨. 딱 지금 현재 블록 상태에서 계산해야 함.
OUT은 GEN과 (현재 IN - KILL) 의 합집합!! 이다.
현재 IN 원소 중에 KILL 원소가 모두 포함되지 않은 경우도 있는데, 그때는 현재 IN에 있는 KILL 원소만 지워주면 된다.
이걸 반복하다보면 OUT 값에 변화가 없는 지점이 오는데, 이때 loop가 종료된다.
(일단 제 시험 공부용으로 한건데, 혹시! 틀린 부분이 있을수도 있으니 본인 교재를 참고하시는 것을 추천합니다)
다른 예시도 연습해봄
여기서 본 예제이고, 단계별로 설명되어 있어서 참고하기 좋음.

아래부터 ppt 정리 시작합니다

- 데이터 흐름 분석 - 프로그램 실행 경로를 따라 데이터 흐름에 대한 정보를 추출하는 다양한 분석 기법의 모음

- d: 변수의 값이 새로 정의되거나 업데이트 되는 프로그램
- d reaches: d가 프로그램의 다른 지점 p에 도달하려면 d에서 p로 가는 경로가 있어야 함. d가 경로상에서 killed되지 않아야.
- killed: 정의된 변수가 같은 경로에서 다시 정의되는 경우
- 목표: 각 지점 p, p까지 도달할 수 있는 모든 정의 d를 찾음. 변수의 유효 범위를 결정하고 최적화 및 오류 검출에 활용.
- 예시 그림에서
- 정의 d: x=1, 프로그램의 초기 정의 지점
- 도달 조건, 정의 변수 x가 경로를 따라 다시 정의되지 않음.
- 따라서, d는 경로를 따라 지점 p에 도달 가능함

loop를 반복해서 완성된 도달 정의 분석 그래프

- RDA를 활용한 copy propagation
- 특정 프로그램 지점에서 변수 x를 그 값인 a로 대체해서 코드를 최적화 하는 과정
- 해당 프로그램 지점 p에서 변수 x에 도달 가능한 모든 정의가 동일한 값을 할당하고 있어야 가능함
- 예시에서는 d1,d3에서 모두 x에 a를 할당하고 있기 떄문에 p 지점에서 y=x에 x 대신 a를 사용할 수 있음

- RDA를 활용한 Loop Optimization
- 루프 외부에서도 동일한 값을 유지하는 계산이 있다면, 루프 바깥으로 이동시켜 연산을 줄일 수 있음
- loop-invariant code motion이라고 함
- loop-invariant: 루프 불변이란, 루프 내부에서 사용되지만 계산된 값이 루프 반복에 따라 변경되지 않음.
- L2 조건 i<10이 체크되고, 루프 본문은 L3, L4로 구성됨.
- L3: z=x+y는 루프 내에서 사용되지만, 변수 x,y는 루프 외부에서 정의되어 루프 내부에서 갱신되지 않음.
- 따라서, L3: z=x+y는 루프 내부에서 루프 외부로 이동 가능함. 10번 계산을 1번 계산으로 축소.

- RDA는 conservative(보수적)으로 접근해야 한다
- 정확한 경로 분석의 불가능성.
- 프로그램 실행 중 특정 경로를 선택할 수 있는지 정확히 결정하는 것은 불가능(halting problem)
- 실행 시점에 정확히 도달하는 정의를 파악하는 것은 불가능
- conservtive approach
- 컴파일러의 최적화를 위해 도달 가능 정의의 안전한 근사값을 계산해야 한다
- 런타임에서 도달할 수 있는 모든 정의를 포괄한다
- 보수적 접근은 안정성을 위해 필수적이다
- over-approximation에 실패하면
- 안전하지 않은 코드 변환이 발생할 수 있음. 불필요한 정의가 포함될 수 있음.
- 정확한 경로 분석의 불가능성.

- RDA의 목표: 블록의 진입과 진출에서 유효한 정의 집합을 계산하는 것
- in, out의 집합은 각 정의가 포함되거나 아니거나, 그래서 2^(정의 수) 가능성이 있음
- RD 계산
- 일반적인 데이터 흐름 방정식 설정
- 반복적 고정점 알고리즘으로 방정식 해결

- 인커밍 정의: 바로 앞의 모든 블록에서 들어오는 정의를 포함해야 함. (이전 loop에서 정의된)
- 아웃고잉 정의: 블록 내에서 새로 생성된 정의 포함.
- kill된 정의: 재정의된 변수는 이전 정의를 제거해야 함. live 정의를 보존하되, 재정의된 정의는 제거
- 예시에서 d1은 d3에 의해 x 변수가 재정의 되어서 kill됨. out에 포함되지 않음.

- in: 모든 선행 블록 pred(Bi)의 out 정의들의 집합을 합집합으로 계산
- out: 각 블록 B에 대해 데이터 흐름을 계산하는 전달함수 fB의 결과값
- 블록 Bi 내에서 새롭게 생성된 집합 gen(Bi)를 포함. in(Bi)에서 현재 블록에서 kill된 정의를 제외한 값을 추가함.
- pred: 블록 Bi의 선행블록 집합. B->Bi로 연결된 블록들의 집합
- fB: 각 블록에 대한 transfer function. 블록 내의 데이터 흐름을 정의하고 계산
- gen(B): 현재 블록 B에서 생성된 정의 집합
- kill(B): 현재 블록 B에서 제거된 정의 집합. 해당 블록 내에서 재정의된 변수들.

각 블록에 대한 in, out값을 표현한 것.
in은 해당 블록으로 들어오는 블록들의 out값의 합집합
out은 해당 블록의 in 값을 fB 함수에 적용한 것.

gen: 해당 블록에서 생성된 정의의 집합
kill: 해당 블록에서 죽은 정의의 집합

- gen: 블록B 내에서 생성된 정의 {d2}. d2는 블록 내에서 마지막으로 변수 a를 정의
- kill: 블록B에서 제거된 정의. {d1,d2} d1,d2는 서로 같은 변수 a를 정의하며, 한 정의는 다른 정의를 덮어쓴다

- 각 블록의 gen과 kill을 구한다 (자세한 과정은 맨 위 손글씨로 증명했음)

- 블록 Bi의 in은 모든 선행 블록 P의 out들의 합집합
- 블록 Bi의 out은 gen(Bi)와 in(Bi) 중 kill되지 않은 정의. 들의 합집합
- fix F: 고정점. 각 블록의 in, out의 변화가 없을 때까지 계산을 반복한다.

- 모든 블록에 대해 in, out을 공집합으로 초기화한다
- while문 시작
- 모든 블록의 in, out의 변화가 없을 때까지 실행한다
- 모든 블록에 대해 in은 선행 블록 out의 집합으로, out은 생성정의와 죽은 정의를 제외한 in 정의의 집합으로 계산.
Liveness Analysis

아래에서 슬라이드 따라서 다시 설명하겠지만
live 변수 분석은 마지막 블록부터 역순으로 진행해야 함.
out은 "후속블록"의 in의 합집합이고, in은 블록에서 사용된 live 변수와 (in-블록 내 정의변수)의 합집합이다.

- live: 어떤 프로그램 지점 p 이후의 프로그래밍 실행 경로에서 변수가 사용되는 경우, live 변수라고 한다.
- dead: p 이후 모든 경로에서 변수가 사용되지 않으면 dead 변수라고 한다
- 각 블록에 대해 live 변수의 집합을 계산하는 것이 liveness analysis의 목표.
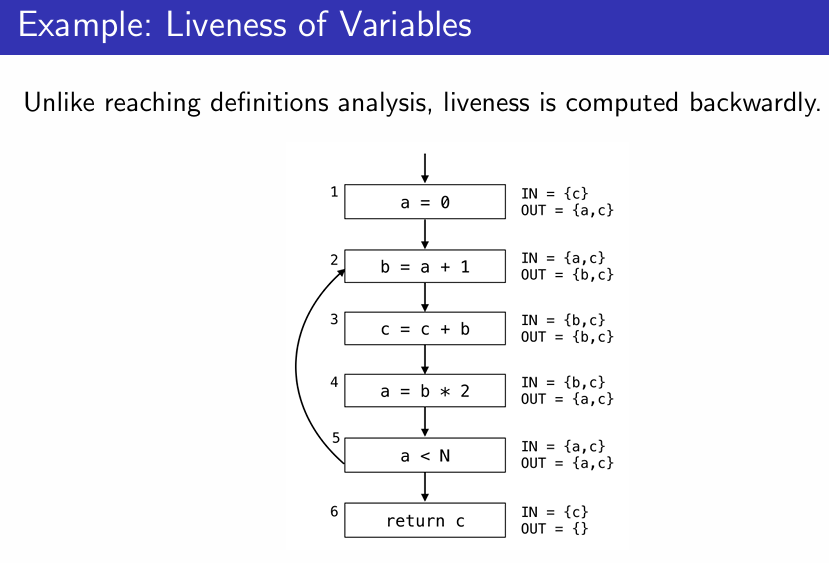
- 도달 가능 정의 분석과 달리 liveness는 backward로 분석한다.

- Liveness 분석 활용
- Deadcode elimination: 사용되지 않는 변수에 대한 할당문을 제거해 불필요한 연산 줄임
- 프로그램에 n: x=y+z라는 할당문이 있지만, x가 dead라면 할당문을 제거할 수 있음.
- 초기화되지 않은 변수 탐지: 프로그램 시작점에서 live 변수인데 초기화 되지 않은 변수. 함수 매개변수는 초기화로 간주함.
- Register 할당: 두 변수 a,b가 같은 시점에 live가 아니라면 동일한 레지스터를 공유해서 사용해도 됨
- Deadcode elimination: 사용되지 않는 변수에 대한 할당문을 제거해 불필요한 연산 줄임

- Liveness 분석에서 in, out 집합은 각 변수를 포함 하냐 마냐로 나뉘기 때문에 2^var의 가능성이 있음
- 이 역시 data-flow 방정식을 세우고, 반복 고정점 알고리즘 방정식을 만들어서 불변지점을 찾는 방식으로 푼

- 직관적 이해
- exit 지점에서 live 변수 조건: 다음 블록에서 사용될 수 있는 변수 포함
- entry 지점에서 live 변수 조건: 블록 B 안에서 사용된 변수 useB를 포함해야 함
- entry 지점에서 외부 변수 유지 조건: 블록 B에서 정의되지 않은 변수 defB는 유지되어야 함
- 데이터 플로우 방정식
- in B: useB(블록 B에서 사용된 live 변수 집합), outB에서 블록 B에서 정의된 변수 defB를 제외한 변수의 합집합.
- out B: 블록 B의 후속 블록 집합(블록 B에서 도달할 수 있는 다음 블록)의 in(S)의 합집합
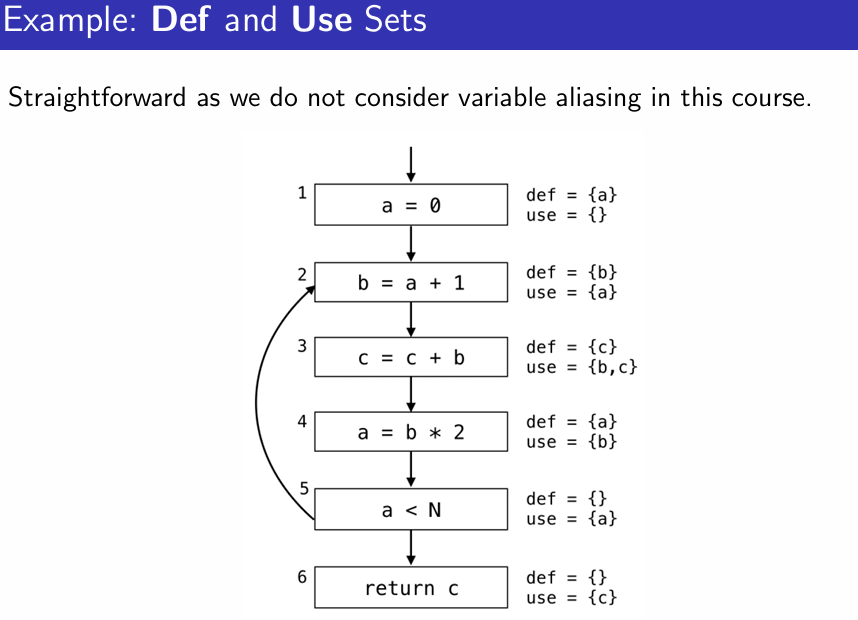

- in, out을 공집합으로 초기화
- while문 진입
- in,out에 변화가 없을 때까지 in,out을 구한다

- use,def를 정의한 후, out/in이 변하지 않을 때까지 반복한다
Availabe Expression Analysis

- Availabe expressions anaylsis
- available expression이란?
- x+y 표현식이 특정 지점 p에서 available하려면
- 모든 경로에서 p에 도달하기 전 x+y가 이미 계산되어 있어야 함
- p에 도달하기 전 x나 y의 값이 재정의되지 않아야 함. x+y 결과가 유효해 다시 계산할 필요 없음.
- x+y 표현식이 특정 지점 p에서 available하려면
- 활용: common subexpression elimination: CSE
- 동일한 표현식을 반복 계산하는 것을 방지하여 성능을 최적화한다
- 프로그램에서 동일한 표현식이 여러 번 계산되어도, 최초 계산 결과를 재사용할 수 있는 경우 중복 계산 제거
- available expression이란?

- in, out에는 expression이 포함되냐, 아니냐에 따라 2^expr의 가능성
- 얘도 마찬가지로 data-flow 방정식 정의하고, 반복 고정점 알고리즘 방정식 만들어서 계산

- program entry: 프로그램 시작점이라 사용가능한 표현식 없음
- 선행 블록: 특정 블록의 entry 지점에서 사용 가능한 표현식, 모든 선행 블록의 exit 지점에서 사용 가능한 표현식임.
- 블록 내 표현식: 블록의 exit 지점에서 사용 가능한 표현식. 블록 내에서 계산된 표현식 포함.
- incoming 표현식 유지 및 무효화 처리
- 블록 exit 지점에서 entry로 들어온 사용가능 표현식 중, 블록 내부에서 값이 변경되거나 무효화되면 exit때 제거.

- in(Entry): 공집합. 시작점에는 사용가능표현식 없음
- in(B): 선행 블록의 out의 합집합
- out(B): 현재 블록에서 계산된 표현식과 in에서 무효화된 표현식을 제외한 표현식의 합집합.

- gen: 특정 블록에서 생성된 유효햔 표현식. 해당 블록에서 다시 무효화되지 않은 표현식의 집합.
- kill: 특정 블록에서 무효화될 수 있는 변수로 인해 더 이상 유효하지 않게 되는 표현식 집합. 블록에서 변수가 "재정의"
- 주의
- 어떤 배열의 원소에 변수를 할당할 때는, 그 배열 원소를 포함하는 표현식이 kill 되어야 한다.
- x=y+z는 y+z를 생성하지만, y=y+z는 y가 subsequently killed되기 떄문에 생성되는게 없다

우측은 슬라이드 아래에 나온 예시를 풀이한 것.
블록 내에서 위에서 아래로 스캔하면서 gen과 kill을 찾음
근데 재정의 때문에 다 날라가서 gen은 공집합이 된다(자세한건 손글씨 참조)

- in(Entry)는 공집합
- in, out은 각 블록의 표현식으로 초기화
- while문 진입
- in, out에 더이상 변화가 없을 때까지 반복
- in: 선행 블록의 out의 합집합
- out: 현재 블록에서 생성된 표현식, in에서 현재 블록에서 무효화된 표현식을 제거한 것의 합집합.
'전공 > 프로그래밍 언어 및 컴파일러' 카테고리의 다른 글
| Lec18. Register Allocation - 15주차 2강 (2) | 2024.12.15 |
|---|---|
| Lec16.Optimization (1) - 14주차 2강 (0) | 2024.12.10 |
| Lec15.lR Translation (2) - 14주차 2강 (0) | 2024.12.10 |
| Lec14.IR Translation (1) - 14주차 1강 (0) | 2024.12.10 |
| Lec13.Semantic Analysis (4) - 13주차 1강/2강 (6) | 2024.12.09 |



